Water, pH, and Non-Covalent Bonding

pH questions

Below are a few sample questions to elucidate the concepts discussed in the book.

• A simple pH problem
• pH of a weak acid
• A buffer problem
• A more involved buffer problem

A simple pH problem

What is the pH 0.1 M HCl?

Answer:

The pH of a solution is the negative logarithm of the concentration of H⁺ ions. In this case, HCl is a very strong acid. HCl completely dissociates to H⁺ and Cl^-.

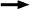HCl H⁺+ Cl^-

The concentration of HCl is 0.1 M, if all of it dissociates to H⁺, then

[H⁺] = 0.1

-log(0.1) = 1.26

pH = 1.26

Remember that a pH of 7 is neutral, and that the pH scale is logarithmic, meaning each pH unit represents a factor of 10. This HCl solution has a difference of 5.74 pH units from water (7 - 1.26). Taking the inverse log of 5.74 means that this HCl solution is more than 500,000 times as acidic as water!

pH of a weak acid solution

What is the pH of a 0.05 M solution of acetic acid? (The K_a of acetic acid = 1.8 x 10^-5)

Answer:

Determining the pH of a weak acid solution is more complicated than for a strong acid. This is because a weak acid does not completely dissociate.

CH₃COOH H⁺ + CH₃COO^-

To simplify matters, it is helpful to construct a grid:

Reaction	CH3COOH	H+	CH3COO-
Initial	0.05 M	0 M	0 M
Change	(-x) M	+ x M	+x M
Equilibrium	(0.05-x) M	x M	x M

To determine the [H⁺], we must employ the K_a of acetic acid, which is 1.8 x 10^-5.

Ka =

[H+][CH3COO-] [CH3COOH]

= 1.8 x 10-5

Substituting the equilibrium values in the table above, we get:

1.8 x 10 -5 =

(x M)(x M) (0.05 - x) M

Since acetic acid is a weak acid, we can assume that very little of it will dissociate. This simplifies the above equation to:

1.8 x 10 -5 =

(x M)(x M) 0.05 M

This can be easily solved:

Now that we have the [H⁺], we can solve for pH:

Buffer Problem

Question 1: What is the ratio of [lactate]/[lactic acid] at pH = 5? (The pK_a of lactic acid = 3.85)

Answer:

To solve this problem, we need to utilize the Henderson-Hasselbalch equation:

pH =

pKa + log

[H+][A-] [HA]

Table 3.3 in the book lists the pKa of lactic acid as 3.85. Now just substitute into the equation:

5 =

3.85 + log

[lactate] [lactic acid]

14 =	[lactate] [lactic acid]

There is 14 times as much lactate as lactic acid at pH 5.

Question 2: What happens if 2 ml of 100 mM HCl is added to 100 ml of a 10 mM solution of phosphoric acid at pH = 7?

Answer:

This is a more involved problem. The first thing to realize is that phosphoric acid is polyprotic, meaning it has more than one H⁺ to donate, and therefore more than one pK_a.

	pKa1		pKa2		pKa3
H3PO4		H2PO4- + H+		HPO4-2+ H+		PO4-3 + H+

Since this problem is at pH = 7, it is the pK_a2 value that is important, for this is the pKa nearest the pH.

First we need to find the ratio of [HPO₄^-2]/[H₂PO₄^-]:

Again, use the Henderson-Hasselbalch equation:

We know we have a total of

that at pH = 7 is made up of HPO₄^-2 and H₂PO₄^-. ( Note 10 mM = 0.01 moles/L and 100 mL = 0.1 L)

So far, this problem is much like the previous one. Now let's answer the question about the addition of 1 ml of 0.1 M HCl. From the high pK_a2 value, we know that phosphoric acid is a weak acid. It will react completely with the HCl (which is the same as H⁺ in solution):

	pKa3
HPO42- + H+		H2PO4-

By adding 2 ml of 0.1 M HCl, we are adding:

(1 x 10^-3 L) X (100 mmoles/L) = 0.2 mmoles H⁺

If we set up the grid as shown above,

Reaction	HPO4-2	H+	H2PO4-
Initial	0.6 mmoles	0.2 mmoles	0.4 M
Change	- 0.2 mmoles	- 0.2 mmoles	+ 0.2 M
Change after equilibrium	0.4 mmoles	0 mmoles	0.6 M

What is the pH of the phosphoric acid solution after the addition of HCl? Again, use the Henderson-Hasselbalch equation to solve

Note that this is not a big change. This is because of phosphoric acid is a buffer near its pK_a and as such is able to resist changes in pH.